Модель ценообразования опционов Блэка–Шоулза (англ. Black–Scholes Option Pricing Model, OPM) — это модель, которая определяет теоретическую цену на европейские опционы, подразумевающая, что если базовый актив торгуется на рынке, то цена опциона на него неявным образом уже устанавливается самим рынком. Данная модель получила широкое распространение на практике и, помимо всего прочего, может также использоваться для оценки всех производных бумаг, включая варранты, конвертируемые ценные бумаги, и даже для оценки собственного капитала финансово зависимых фирм.

Согласно Модели Блэка-Шоулза, ключевым элементом определения стоимости опциона является ожидаемая волатильность базового актива. В зависимости от колебания актива, цена на него возрастает или понижается, что прямопропорционально влияет на стоимость опциона. Таким образом, если известна стоимость опциона, то можно определить уровень волатильности ожидаемой рынком.

Описание модели ценообразования опционов Блэка-Шоулза

В октябре 1997 года Нобелевская премия по экономике была присуждена Роберту Мертону (Robert Merton) и Майрону Шоулзу (Myron Scholes). Комитет по назначению лауреатов выдвинул для присуждения премии еще одного ученого, Фишера Блэка (Fisher Black), но его преждевременная смерть в 1995 г. в возрасте 57 лет помешала ему разделить эту честь. Эти три человека считаются создателями математической формулы для вычисления стоимости опционов и других производных иструментов, которая оказала огромное влияние на развитие теории и практики финансов. Эта формула сегодня широко известна как формула Блэка-Шоулза (Black-Scholes option pricing formula).

Открытие данной формулы привело к повышенному интересу к производным инструментам и взрывному росту опционной торговли. Опубликование формулы Блэка-Шоулза в 1973 г. позволило отойти от субъективно-интуитивных оценок при определении цены опционов и подвести под него теоретическую базу, применимую и к другим производным инструментам. Для начала 70-х сама идея использовать математический подход для оценки производных инструментов была революционна.

Современное управление рисками, применяемое в страховании, торговле на фондовом рынке и инвестировании, основывается на возможности использовать математические методы для предсказания будущего. Конечно, не со 100%-ной вероятностью, но достаточно точно для того, чтобы принять взвешенное инвестиционное решение. Основополагающий принцип работы на финансовых рынках состоит в следующем: чем больший риск вы готовы на себя принять, тем на большее вознаграждение вы вправе рассчитывать. Использование математики никогда не сможет полностью элиминировать риск, но может помочь правильно оценить степень принимаемого на себя риска и решить вопрос о справедливом вознаграждении.

Шесть допущений теории

Чтобы вывести свою модель ценообразования опционов, Блэк и Шоулз сделали следующие предположения:

• По базисному активу опциона call дивиденды не выплачиваются в течение всего срока действия опциона.
• Нет транзакционных затрат, связанных с покупкой или продажей акции или опциона.
• Краткосрочная безрисковая процентная ставка известна и является постоянной в течение всего срока действия опциона.
• Любой покупатель ценной бумаги может получать ссуды по краткосрочной безрисковой ставке для оплаты любой части ее цены.
• Короткая продажа разрешается без ограничений, и при этом продавец получит немедленно всю наличную сумму за проданную без покрытия ценную бумагу по сегодняшней цене.
• Торговля ценными бумагами (базовым активом) ведется непрерывно, и поведение их цены подчиняется модели геометрического броуновского движения с известными параметрами.

Вывод модели основывается на концепции безрискового хеджирования. Покупая акции и одновременно продавая опционы call на эти акции, инвестор может конструировать безрисковую позицию, где прибыли по акциям будут точно компенсировать убытки по опционам, и наоборот.

Безрисковая хеджированная позиция должна приносить доход по ставке, равной безрисковой процентной ставке, в противном случае существовала бы возможность извлечения арбитражной прибыли и инвесторы, пытаясь получить преимущества от этой возможности, приводили бы цену опциона к равновесному уровню, который определяется моделью.

Формулы

Цена (европейского) опциона call: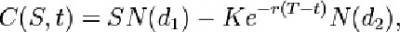

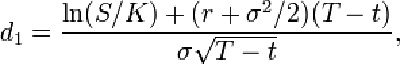
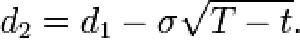
Цена (европейского) опциона put:

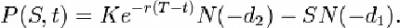
Обозначения:

C(S,t) — текущая стоимость опциона call в момент t до истечения срока опциона;
S — текущая цена базисной акции;
N(x) — вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения) (Для определения N(x) можно использовать таблицы для стандартной нормальной кривой или Excel-функцию HOPMCTPACП(x). Она возвращает стандартное нормальное интегральное распределение, которое имеет среднее, равное нулю, и стандартное отклонение, равное единице);
K — цена исполнения опциона;
r — безрисковая процентная ставка;
T— t - время до истечения срока опциона (период опциона);
σ — волатильность (квадратный корень из дисперсии) базисной акции.

«Греки»

Для характеристики чувствительности цены (премии) опциона к изменению тех или иных величин, применяют различные коэффициенты, называемые «греками». Название происходит от греческого алфавита, буквами которого обозначаются эти коэффициенты (за исключением «веги»). «Греки» в рамках модели Блэка-Шоулза вычисляются явным образом: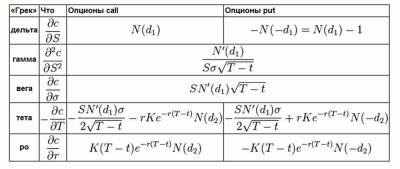

Примечательно, что формулы гамма и вега одинаковы для опционов пут и колл, что является логическим выводом теории паритета опционов пут и колл.

Например, знание коэффициентов «дельта» Δ и «гамма» Γ позволяют оценить изменение цены (премии) опциона δc при изменении цены финансового инструмента δS, лежащего в основе опциона: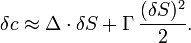

Эта формула получается при помощи разложения в ряд Тейлора цены опциона c(S). Аналогично, чем больше «тета», тем быстрее происходит временной распад опциона, и т.д.

Википедия